Leewooguebou's Eden

Stability Circle Explained(Math Warning)

By

Stable, what a beautiful word! With OPAMP in a “stable” circuit, we don not need to worry about oscillation and so many other problems. However, under many circumstances, circuits we design are not stable, which we call “conditionally stable”. In this article, we’ll find out what stability is and how it is related to RF amplification design.

Power gain in a two-port amplifier

Figure 1. Diagram of a two-port amplifier

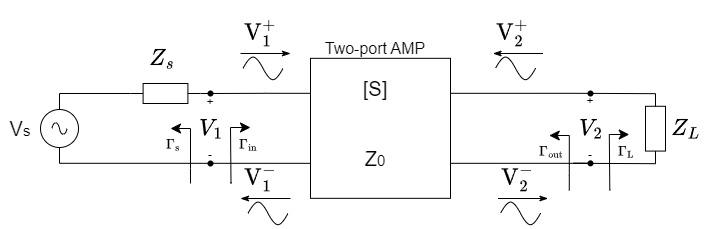
Figure 1 shows a diagram of a two-port amplifier

Before doing mathematical calculations, we shall define three different two-port power gains as follows:

  • Power\,\,gain=G=\small{{{P_L}\Bigg/{P_m}}} It is the ratio of power dissipated in the load to the power delivered to the input of the two-port network and is independent of Z_s(though characteristics of some active devices depend on its load), which means that it can be derived with \left[ S \right], Z_0 and Z_L.
  • Available\,\,power\,\,gain=G_A=\small{{{P_{avn}}\Bigg/{P_{avs}}}} It is the ratio of the power available from the two-port network to the power available from the source. This gain assumes conjugate matching on both source and load side, which means it depends on Z_s and Z_L=Z_0.
  • Transducer\,\,power\,\,gain=G_T={{P_L}\Bigg/{P_{avs}}} It is the ratio of the power delivered to the load to the power available from the source. It depends on both Z_s and Z_L.

When load side and source side are both conjugate matched, we have G=G_A=G_T.

Gain Calculation

The reflection coefficient seen looking toward the load is

\varGamma _L=\frac{Z_L-Z_0}{Z_L+Z_0}

while the reflection coefficient looking toward the source is

\varGamma _s=\frac{Z_s-Z_0}{Z_s+Z_0}

Generally, both sides of the amplifier are not well matched and we can derive V_{1}^{-} and V_{2}^{-}.

V_{1}^{-}=S_{11}V_{1}^{+}+S_{12}V_{2}^{+}=S_{11}V_{1}^{+}+S_{12}\varGamma _LV_{2}^{-} \\ V_{2}^{-}=S_{21}V_{1}^{+}+S_{22}V_{2}^{+}=S_{21}V_{1}^{+}+S_{22}\varGamma _LV_{2}^{-} //

then we can derive \varGamma _{in} and \varGamma _{out}

\varGamma _{in}=\frac{V_{1}^{-}}{V_{1}^{+}}=S_{11}+\frac{S_{12}S_{21}\varGamma _L}{1-S_{22}\varGamma _L}=\frac{Z_{in}-Z_0}{Z_{in}+Z_0} \\ \varGamma _{out}=\frac{V_{2}^{-}}{V_{2}^{+}}=S_{22}+\frac{S_{12}S_{21}\varGamma _s}{1-S_{11}\varGamma _s}

From voltage division

V_1=V_s\frac{Z_{in}}{Z_s+Z_{in}}=V_{1}^{+}+V_{1}^{-}=V_{1}^{+}\left( 1+\varGamma _{in} \right)

and by the definition of reflection coeficient

Z_{in}=Z_0\frac{1+\varGamma _{in}}{1-\varGamma _{in}}

If we solve V_{1}^{+} in terms of V_s, then it gives

V_{1}^{+}=\frac{V_s}{2}\frac{1-\varGamma _s}{1-\varGamma _s\varGamma _{in}}

and if peak values are assumed for all voltages, the average power delivered to the network is

P_{\mathrm{in}}=\frac{1}{2Z_0}\left| V_{1}^{+} \right|^2\left( 1-\left| \Gamma _{\mathrm{in}} \right|^2 \right) =\frac{\left| V_s \right|^2}{8Z_0}\frac{\left| 1-\Gamma _s \right|^2}{\left| 1-\Gamma _s\Gamma _{\mathrm{in}} \right|^2}\bigl( 1-\left| \Gamma _{\mathrm{in}} \right|^2 \bigr)

As for the power delivered to the load

P_L=\frac{|V_{2}^{-}|^2}{2Z_0}\left( 1-|\varGamma _L| \right) \\ V_{2}^{-}=\frac{S_{21}V_{1}^{+}}{1-S_{22}\varGamma _L} \\ P_L=\frac{V_{1}^{+}}{2Z_0}\frac{|S_{21}|^2\left( 1-|\varGamma _L|^2 \right)}{|1-S_{22}\varGamma _L|}=\frac{|V_s|^2}{8Z_0}\frac{|S_{21}|^2\left( 1-|\varGamma _L|^2 \right) |1-\varGamma _s|^2}{|1-S_{22}\varGamma _L|^2|1-\varGamma _s\varGamma _{in}|^2}

so power gain is

G=\frac{P_L}{P_{in}}=\frac{|S_{21}|^2\left( 1-|\varGamma _L|^2 \right)}{\left( 1-|\varGamma _{in}|^2 \right) |1-S_{22}\varGamma _L|^2}

If we are calculating available power gain, there should be conjugate matching on the source side, which means

Z_s=Z_{in}^{*} \\ \varGamma _{in}=\frac{Z_{in}-Z_0}{Z_{in}+Z_0} \\ \varGamma _s=\frac{Z_s-Z_0}{Z_s+Z_0} \\ \varGamma _{s}^{*}=\frac{\left( Z_s-Z_0 \right) ^*}{\left( Z_s-Z_0 \right) ^*}=\frac{Z_{s}^{*}-Z_0}{Z_{s}^{*}+Z_0}=\frac{Z_{in}-Z_0}{Z_{in}+Z_0}=\varGamma _{in}

and when

\varGamma _{in}=\varGamma _{s}^{*} \\ P_{avs}=P_{in}=\frac{|V_s|^2}{8Z_0}\frac{|1-\varGamma _s|^2}{\left( 1-|\varGamma _s|^2 \right)}

Similarly, when there is conjugate matching on the load side,

\varGamma _L=\varGamma _{out}^{*} \\ P_{avn}=P_L=\frac{|V_s|^2}{8Z_0}\frac{|S_{21}|^2\left( 1-|\varGamma _{out}|^2 \right) |1-\varGamma _s|^2}{|1-S_{22}\varGamma _{out}^{*}||1-\varGamma _s\varGamma _{in}|^2}

However, \varGamma _{in} must be evaluated for \varGamma_L=\varGamma_{out}^{*} so it can be shown that

\varGamma _{in}=S_{11}+\frac{S_{12}S_{21}\varGamma _L}{1-S_{22}\varGamma _L} \\ \varGamma _{out}=S_{22}+\frac{S_{12}S_{21}\varGamma _s}{1-S_{11}\varGamma _s} \\ \varGamma _{out}\varGamma _L=S_{22}\varGamma _L+\frac{S_{12}S_{21}\varGamma _L\varGamma _s}{1-S_{11}\varGamma _s} \\ \left( 1-S_{11}\varGamma _s \right) \left( |\varGamma _{out}|^2-S_{22}\varGamma _L \right) =S_{12}S_{21}\varGamma _L\varGamma _s \\ 1-\varGamma _s\varGamma _{in}=1-S_{11}\varGamma _s-\frac{S_{12}S_{21}\varGamma _L\varGamma _s}{1-S_{22}\varGamma _L}=\frac{\left( 1-S_{22}\varGamma _L \right) \left( 1-S_{11}\varGamma _s \right)}{1-S_{22}\varGamma _L}-\frac{S_{12}S_{21}\varGamma _L\varGamma _s}{1-S_{22}\varGamma _L}=\frac{\left( 1-S_{11}\varGamma _s \right) \left( 1-S_{22}\varGamma _L-|\varGamma _{out}|^2+S_{22}\varGamma _L \right)}{1-S_{22}\varGamma _L}=\frac{\left( 1-S_{11}\varGamma _s \right) \left( 1-|\varGamma _{out}|^2 \right)}{1-S_{22}\varGamma _L} \\ |1-\varGamma _s\varGamma _{in}|^2=\frac{|1-S_{11}\varGamma _s|^2\left( 1-|\varGamma _{out}|^2 \right) ^2}{|1-S_{22}\varGamma _{out}^{*}|^2}

and P_{avn} reduces to

P_{avn}=\frac{|V_s|^2}{8Z_0}\frac{|S_{21}|^2|1-\varGamma _s|^2}{|1-S_{11}\varGamma _s|^2\left( 1-|\varGamma _{out}|^2 \right)}

Now both P_{avn} and P_{avs} have been expressed in terms of the source voltage V_s, which is independent of impedances.

So, the available and transducer power gain is

G_A=\frac{P_{avn}}{P_{avs}}=\frac{|S_{21}|^2\left( 1-|\varGamma _s|^2 \right)}{|1-S_{11}\varGamma _s|^2\left( 1-|\varGamma _{out}|^2 \right)} \\ G_T=\frac{P_L}{P_{avs}}=\frac{|S_{21}|^2\left( 1-|\varGamma _s|^2 \right) \left( 1-|\varGamma _L|^2 \right)}{|1-\varGamma _s\varGamma _{in}|^2|1-S_{22}\varGamma _L|^2}

When both source side and load side are matched(\varGamma _s=\varGamma _L=0), we have

G_A=|S_{21}|^2

When S_{12}=0, then we have

\varGamma _{in}=S_{11}+\frac{S_{12}S_{21}\varGamma _s}{1-S_{11}\varGamma _s}=S_{11}

and the unilateral transducer power gain can be given in a format with symmetrical beauty and balance.

G_{TU}=\frac{|S_{21}|^2\left( 1-|\varGamma _s|^2 \right) \left( 1-|\varGamma _L|^2 \right)}{|1-S_{11}\varGamma _s|^2|1-S_{22}\varGamma _L|^2}

Single-Stage Amplifier

A single-stage microwave amplifier can be modeled by the circuit in figure 2.

Figure 2. General transistor amplifier circuit

In figure 2,a matching network is added on both source and load side to transform the input and output impedance Z_0 to the source and load impedances Z_s and Z_L. And their effective gain factors can be defined as follows

G_s=\frac{1-|\varGamma _s|^2}{|1-\varGamma _{in}\varGamma _s|^2} \\ G_0=|S_{21}|^2 \\ G_L=\frac{1-|\varGamma _L|^2}{|1-S_{22}\varGamma _L|^2}

and the overall transducer gain is

G_T=G_sG_0G_L

Furthermore, we assume the circuit is unilateral(S_{12}=0). Then

\varGamma _{in}=S_{11} \\ \varGamma _{out}=S_{22} \\ G_s=\frac{1-|\varGamma _s|^2}{|1-S_{11}\varGamma _s|^2} \\ G_0=|S_{21}|^2 \\ G_L=\frac{1-|\varGamma _L|^2}{|1-S_{22}\varGamma _L|^2}

The alternative results can also be derived from small signal model of this circuit.

Stability Circle

In the circuit of figure 2, oscillation may occur if either the input or the output port impedance has a negative real part, which will imply that |\varGamma _{in}|>1 or |\varGamma _{out}|>1. And \varGamma _{in} and \varGamma _{out} depend on the matching networks so the stability of the circuit depends on \varGamma _s and \varGamma _L to be stable. Thus we can define two types of stability:

  • Unconditional stability The network is unconditionally stable when |\varGamma _{in}|<1 and |\varGamma _{out}|<1 for all passive source and load impedances.
  • Conditional stability The network is conditionally stable when |\varGamma _{in}|<1 and |\varGamma _{out}|<1 only for a certain range of passive source and load impedances. It is also referred to as potentially unstable.

Besides, the stability condition of an amplifier circuit is usually frequency dependent. It is therefore possible for an amplifier to be stable at its design frequency but unstable at other frequencies.

When a circuit is unconditionally stable, we have

|\varGamma _{in}|=|S_{11}+\frac{S_{12}S_{21}\varGamma _L}{1-S_{22}\varGamma _L}|<1 \\ |\varGamma _{out}|=|S_{22}+\frac{S_{12}S_{21}\varGamma _s}{1-S_{11}\varGamma _s}|<1

If the circuit is unilateral, the conditons above can be reduced to

|S_{11}|<1 \\ |S_{22}|<1

Otherwise, the inequalities define a range of values for \varGamma _s and \varGamma _L where the amplifier will be stable. And in smith chart we can find that. The stability circles are defined as the loci in the \varGamma _L (or \varGamma _s) plane for which |\varGamma _{in}|=1 (or |\varGamma _{out}|=1).

We can derive the equation for the output stability circle as follows.

|\varGamma _{in}|=|S_{11}+\frac{S_{12}S_{21}\varGamma _L}{1-S_{22}\varGamma _L}|=1 \\ |S_{11}\left( 1-S_{22}\varGamma _L \right) +S_{12}S_{21}\varGamma _L|=|1-S_{22}\varGamma _L|

Now we define \varDelta as the determinant of the scattering matrix

\varDelta =S_{11}S_{22}-S_{12}S_{21}

Then the output stability circle can be written as

|S_{11}-\varDelta \varGamma _L|=|1-S_{22}\varGamma _L|

and we square both sides and simplify

|S_{11}|^2+|\varDelta |^2|\varGamma _L|^2-\left( \varDelta \varGamma _LS_{11}^{*}+\varDelta ^*\varGamma _{L}^{*}S_{11} \right) =1+|S_{22}|^2|\varGamma _L|^2-\left( S_{22}^{*}\varGamma _{L}^{*}+S_{22}\varGamma _L \right) \\ \left( |S_{22}|^2-|\varDelta |^2 \right) \varGamma _L\varGamma _{L}^{*}-\left( S_{22}-\varDelta S_{11}^{*} \right) \varGamma _L-\left( S_{22}^{*}-\varDelta ^*S_{11} \right) \varGamma _{L}^{*}=|S_{11}|^2-1 \\ \varGamma _L\varGamma _{L}^{*}-\frac{\left( S_{22}-\varDelta S_{11}^{*} \right) \varGamma _L+\left( S_{22}^{*}-\varDelta ^*S_{11} \right) \varGamma _{L}^{*}}{|S_{22}|^2-|\varDelta |^2}=\frac{|S_{11}|^2-1}{|S_{22}|^2-|\varDelta |^2}

And we add |S_{22}-\varDelta S_{11}^{*}|^2/\left( |S_{22}|^2-|\varDelta |^2 \right) ^2 to both sides.

|\varGamma _L-\frac{\left( S_{22}-\varDelta S_{11}^{*} \right) ^*}{|S_{22}|^2-|\varDelta |^2}|=|\frac{S_{12}S_{21}}{|S_{22}|^2-|\varDelta |^2}|

In the complex \varGamma plane, an equation of the form |\varGamma -C|=R represents a circle centered at C and a radius R. We define the output stability circle as follows:

C_L=\frac{\left( S_{22}-\varDelta S_{11}^{*} \right) ^*}{|S_{22}|^2-|\varDelta |^2} \\ R_L=|\frac{S_{12}S_{21}}{|S_{22}|^2-|\varDelta |^2}|

Similarly, the input stability circle can be defined as:

C_s=\frac{\left( S_{11}-\varDelta S_{22}^{*} \right) ^*}{|S_{11}|^2-|\varDelta |^2} \\ R_s=|\frac{S_{12}S_{21}}{|S_{11}|^2-|\varDelta |^2}|

Now we know how to draw a stability circle and we know on the one side of the circle, the circuit is stable while on the other side, it’s not. Here comes the question: which side is stable and which side is unstable?

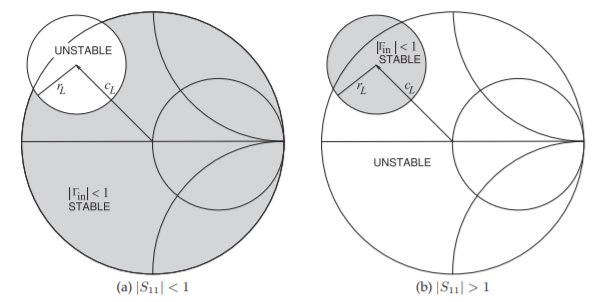
Consider the output stability circle plotted as figure 3 shows in the complex \varGamma _L plane. Let’s suppose S_{21}S_{12}=0. Then R_L=0, which means the amplifier is either unconditionally stable or unconditionally unstable.

Figure 3. Output stability circle for a conditionally stable device[source]

Now we go back to the origin equation

|\varGamma _{in}|=|S_{11}+\frac{S_{12}S_{21}\varGamma _L}{1-S_{22}\varGamma _L}|=|S_{11}|
  • |S_{11}|<1 The circuit is unconditionally stable, which means under this condition, the area out of the circle is stable.
  • |S_{11}|>1 The circuit is unconditionally unstable, which means under this condition, the area in the circle is stable.

This result is shown in figure 3.

Test for Unconditional Stability

The stability circle is a way to determine where the amplifier will will be unstable in the complex reflection coefficient plane. However, there is a simple way to determine unconditional stability, which is K-Δ test.

K=\frac{1-|S_{11}|^2-|S_{22}|^2+|\varDelta |^2}{2|S_{12}S_{21}|}>1 \\ |\varDelta |=|S_{11}S_{22}-S_{12}S_{21}|<1

If the two conditions are met simultaneously, then the amplifier is unconditionally stable.

One Example in ADS

Let’s see an example in ADS which is a single -stage amplifier.

To make an amplifier from a BJT

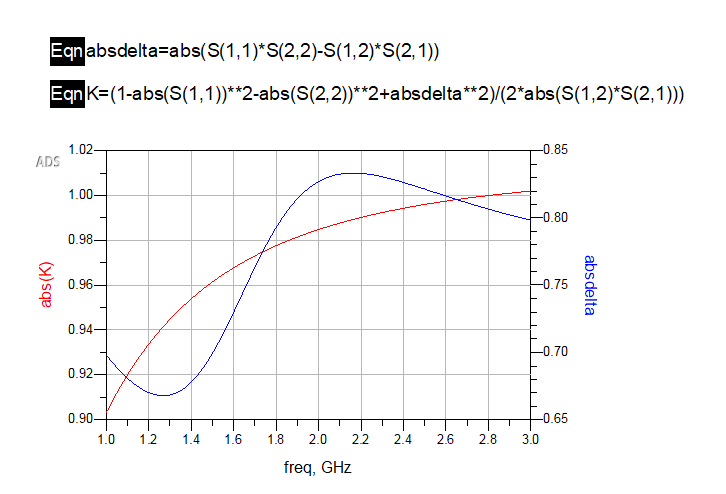
In 07_SP_Matching of this project, we can add two equtions to test its stability as shown in figure 4. We can see the amplifier we design is conditional stable at 2 GHz. We can also use StabFact component to derive K.

Figure 4.K-Δ test

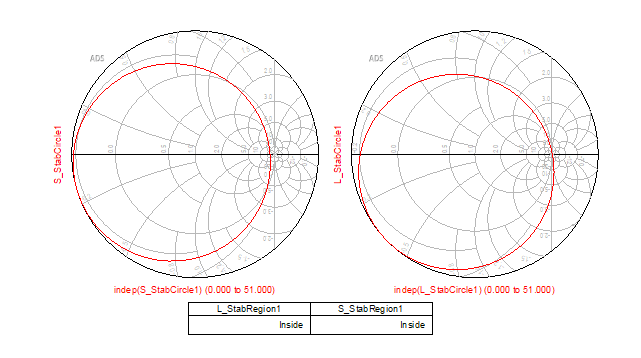
Then let’s see what the stability circle looks like at 2GHz. We can use S_StabCircle and L_StabCircle to draw the circle and use S_StabRegion and L_StabRegion to determine the stable region.

Figure 5. Stabitlity Circle

Reference

Microwave Engineering by David M. Pozar

Leave a comment

This site uses Akismet to reduce spam. Learn how your comment data is processed.