Leewooguebou's Eden

Using open-circuited or short-circuited transmission line(stub) is a popular matching technique. Such a matching technique is easy to fabricated as stubs can be part of transmission lines(microstrip line or stripe line). Besides, lumped components are avoided.

How stubs work

How do stubs work? Using a smith chart, it’s easy to explain.

Before solving a example, it is quite important to know what a shunt stub bring wo the load. As load can be written as and stubs only change the imaginary part, input admittance can be written as , in which jX is susceptance brought by the added stub. Therefore, real part remain the same. Now let’s solve the example 1 below.

Example 1
For a load impedance ,design a single-stub (short or open circuit) shunt tuning network to math this load to a  transmission line. Assuming that the load is matched at 1GHz.

Here is the solution. First, we plot the normalized load . Apparently, real part of the admittance is not 1, and it will never match by inserting shunt stubs alone. So we need to insert a series line first to make normalized conductance equal 0.02. Then by inserting a shunt stub we can make normalized susceptance equal 0.The matching steps can be presented in the smith chart below.

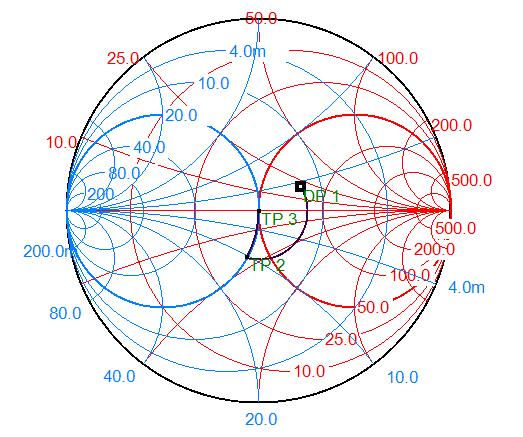
If we insert a longer series line, there is another intersection point on the upper part of the circle ( is the normalized conductance). And for each intersection point, we can match the load by inserting either short-circuit or open-circuit shunt stub. As a result, there are four different matching solutions.

Double-stub tuning network

Okay, now we know how to match with one shunt stub and one series line, then it will be simple to understand how to match with two shunt stubs and one series line with given electrical length. Let’s look at the example 2 below.

Example 2
For a load impedance ,design a double-stub (short or open circuit) shunt tuning network with two stubs spaced λ/4（at 1GHz） to math this load to a  transmission line. Assuming that the load is matched at 1GHz.

For double-stub matching network, we should insert a shunt stub first, then the series line of given length, a shunt stub at last. Instead of thinking forwards, we’d better solve the problem backwards. From the solution of example 1, we know that if a load can be matched with just one shunt stub, the conductance of the load must be 0.02mS. In smith chart, all the points meeting this requirement are a circle. Then there comes the λ/4 series line. It is necessary that after inserting this series line, the point fall on that unity-normalized-conductance circle. For inserting a series line, the point will rotate clockwise 2βl around the center. So in this example, after inserting the first shunt stub, the point should fall on the unity-normalized-resistance circle, which is circle that unity-normalized-conductance circle rotates counter-clockwise 180 degrees.

Then, we can match the load without tuning the electrical length of two shunt stubs.

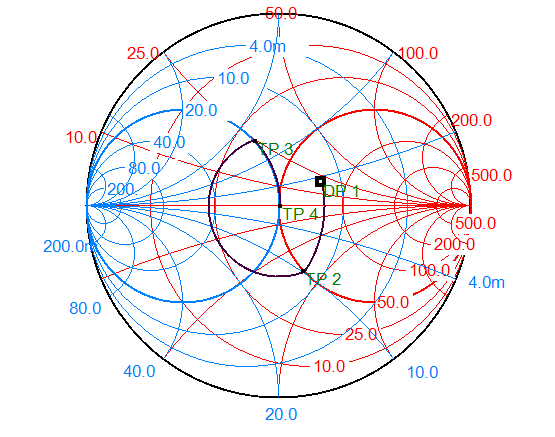
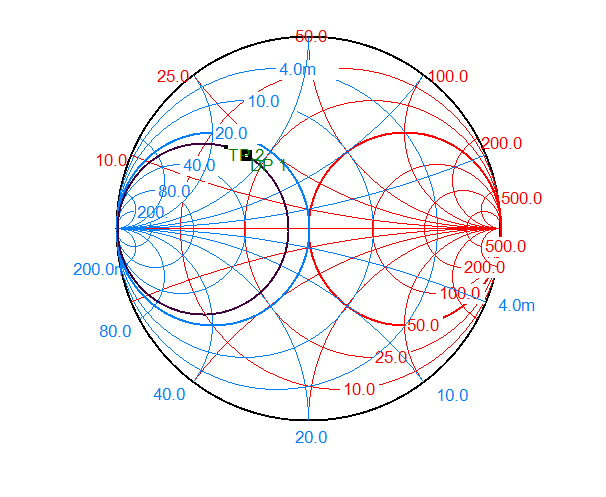
However, if we want to match a load impedance using a double-stub network with two stubs spaced λ/4 （at 1GHz). Then it is impossible, because we can’t make an intersection point on the unity-normalized-resistance circle just by inserting a shunt stub. It means all the load points(resistance less than 50Ω) within the unity-normalized-conductance circle can not be matched using such kind of network. We have to insert a series line to move this point out of that circle first.

Thanks

This is my first blog, thanks for your reading.